上回說明完了廣度優先搜尋(BFS)以及深度優先搜尋(DFS)的概念以及實例了，接著我們就要來講解A*演算法並應用到食人族與傳教士過河的例子上了。

先來看看題目：
有n名食人族、m名傳教士和兩艘船在河的右岸，所有人都希望能夠搭船到左岸過去，A船能夠乘載最多2人，B船能夠承載最多3人。限制為無論何時兩岸的情形，食人族人數都得小於或等於傳教士人數。我們希望能夠得出在不同n值以及不同m值的情況下，過河的最少次數。
這樣的題目在m值和n值都還很小，答案都是顯而易見的，但當m值和n值一大，那結果就變得很難判斷了。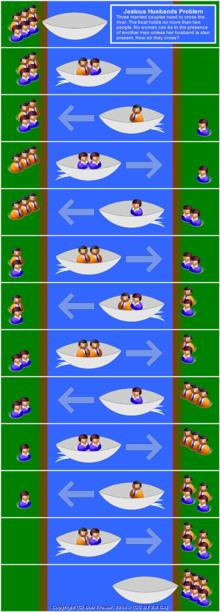

圖片來源：https://zh.wikipedia.org/zh-tw/%E4%BC%A0%E6%95%99%E5%A3%AB%E5%92%8C%E5%90%83%E4%BA%BA%E6%81%B6%E9%AD%94%E9%97%AE%E9%A2%98

接下來介紹A演算法，以函式表達為f(n) = g(n) + h(n)，g(n)代表起點到任意點n的實際距離，h(n)為任意點n到終點的估算距離。在進行推算最佳距離的過程即是以佇列儲存當前節點的展開，我們就是要將之前所講解的廣度優先搜尋在這裡。但廣度優先搜尋僅是利用在節點的展開，而A演算法不一樣的地方在於我們原先做廣度優先搜尋時，同一層的解點展開並沒有優先順序，但A*演算法有了優先順序，也就是上面函式所提及的f值。將f(n)最小值放在佇列前方，以廣度優先搜尋的概念去執行，最終找到原點與終點的最短距離。
而若將g(n)設為0，即是貪婪演算法；h(n)設為0，即為Dijkstra演算法。可以根據不同的情形選用不同種類的演算法。
或許大家看到這裡還有些懵懂，接下來我們就要用傳教士與食人族過河的例子讓大家能夠更加清楚的理解了。